Decidere di fare trading significa impegnarsi in un’attività che comporta dei sacrifici ed un ben determinato bagaglio di conoscenze. D’altro canto se si ripensa all’ora di matematica quando si frequentavano le scuole superiori, se la sensazione che si prova è di gioia, allora si potrebbe pensare un giorno di diventare un serioso ed affidabile analista dei mercati finanziari. Le immagini, invece, che vengono in mente al resto di noi, probabilmente si avvicinano di più al senso di noia o di terrore che provavamo quando contavamo i minuti e i secondi che mancavano alla fine della lezione.
Contributi nella matematica
Come sarebbe stato diverso se soltanto i nostri insegnanti avessero collegato la statistica a qualcosa di vero, come chiudere una posizione short a tre giorni intascando il 15% sullo scambio. Se ai tempi del liceo mi avessero presentato un caso simile, avrei certamente dimostrato un interesse molto maggiore a quei concetti e a quei calcoli solo apparentemente astratti. Per questo motivo risponde ad un atteggiamento di buon senso quello di prestare attenzione a quanto sto descrivendo. Infatti queste tecniche di misurazione della volatilità potrebbero diventare i migliori amici man mano che si procede con l’analisi del movimento del prezzo.
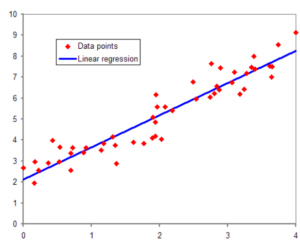
Nel trading la logica del profitto è lo stimolo che esercita l’influenza maggiore. Che il risultato stia nel brivido di un trade di successo o nel denaro, di solito è la logica del profitto che ci guida. Da trader sulla volatilità, è bene riconoscere che stiamo sfruttando golose opportunità del mercato, ed in effetti con la regressione lineare, mentre il pendolo* del prezzo oscilla in avanti e indietro, dobbiamo essere in grado di misurare quanto lontano è “troppo lontano”. D’altro canto con tutta probabilità la cosiddetta regressione lineare è la migliore misura statistica di una serie di dati, o prezzi. Detto in parole semplici, la regressione lineare è il processo matematico che consiste nell’approssimare al meglio una linea retta ad una serie di punti-dati, che nel nostro caso corrispondono alle varie quotazioni registrate dal mercato di riferimento.
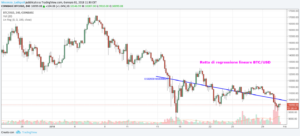
Non vi è davvero alcun bisogno di perdersi in tutte le altre definizioni più complesse di regressione lineare, sebbene esistano molti metodi aridi ed astratti per descriverla, che però ricordano soltanto quegli oscuri insegnanti di matematica della scuola superiore. Nelle figure proposte ciascuna delle linee è circondata da una serie di punti o prezzi dati. I punti tracciati rappresentano una serie di livelli che in un caso corrispondono alle quotazioni di chiusura registrate dal rapporto BTCUSD (Grafico BTCUSD by Tradingview) nel breve termine. Di fatto il processo di regressione lineare consiste nel disegnare una retta che passi attraverso questa serie di punti-dati nel modo più efficace possibile.
Per capire meglio come tutto ciò funzioni, immaginiamo di ripetere il processo di regressione lineare e disegnare la retta con la migliore approssimazione possibile, collegando ciascun punto alla retta orizzontale, utilizzando un filo d’oro a 36 carati. Dopo aver terminato potremmo recuperare l’oro rimasto per cui, ovviamente, si vorrà utilizzare quanto meno filo possibile per collegare tutti questi punti che rappresentano i prezzi. E’ così che la retta viene posizionata nel modo più efficiente. Questa è la regressione lineare. Dal punto di vista tecnico la regressione lineare sfrutta il processo meglio definito “dei minimi quadrati” per adattare nel modo più efficace possibile la retta ai dati, tuttavia quello che ora a noi importa sono i riflessi pratici che la retta in questione esercita sul trading. La regressione lineare viene talvolta confusa con la media mobile ma l’esperienza pratica ci suggerisce che si tratta di due differenti tipi di indicatori che eseguono misurazioni diverse.
La media mobile è un metodo ritardatario: a meno che il movimento del prezzo non mostri una volatilità molto bassa per la maggior parte della durata della media mobile, sarà probabilmente al di sopra o al di sotto della linea della media mobile. Così non è con la regressione lineare: non appena il trend del prezzo comincia a cambiare direzione, la retta di regressione lineare abbraccia più da vicino le candele del prezzo. Ecco spiegato il motivo per cui la regressione lineare viene utilizzata per scopi diversi rispetto alla media mobile. E’ bene sottolineare infatti che la retta di regressione lineare non rappresenta una media, ma piuttosto un sentiero efficiente, non essendo gravata dai valori passati.
Ad esempio se l’intervallo temporale viene spostato avanti di un periodo, allora viene eliminato il dato più vecchio e aggiunto quello nuovo, il che vale sia per la media mobile sia per la regressione lineare. La differenza è che in quest’ultimo caso è l’intera retta ad essere ricalcolata. Tutto cambia, quindi, mentre nel caso della media mobile è soltanto il punto più recente ad assumere un nuovo valore.
Sul versante operativo risulta spesso decisivo il market timing dato dal “troppo lontano” dalla retta; ovvero un’entrata della posizione distante dalla linea di regressione in conformità al principio del ritorno ai valori medi. Short pertanto se il prezzo di mercato è molto al di sopra della linea di regressione e long invece se il prezzo di mercato è molto al di sotto della retta di regressione.
Questo contenuto non deve essere considerato un consiglio di investimento.
Non offriamo alcun tipo di consulenza finanziaria. L’articolo ha uno scopo soltanto informativo e alcuni contenuti sono Comunicati Stampa
scritti direttamente dai nostri Clienti.
I lettori sono tenuti pertanto a effettuare le proprie ricerche per verificare l’aggiornamento dei dati.
Questo sito NON è responsabile, direttamente o indirettamente, per qualsivoglia danno o perdita, reale o presunta,
causata dall'utilizzo di qualunque contenuto o servizio menzionato sul sito https://valutevirtuali.com.

















